A “granny summary” of the article by Dror Dotan and Stanislas Dehaene
Parallel and serial processes in number-to-quantity conversion
Try thinking about 26 ginger cats. Visualize what they look like. Got it? Good. Now think: how did you get from the pair of digits 2,6 that you saw on the screen to the quantity that you visualized? How did you know that the “6” in 26 stands for 6 cats, but the “2” stands for 20 cats? Did you recall what your first-grade math teacher taught you about the decimal system? Probably not. More likely, your response was intuitive: you saw the digit string 26 and just imagined a more-or-less corresponding number of cats. You automatically translated the digit string into quantity.
Such “translation” may be simple for single digits, but with multi-digit numbers it’s harder, because the cognitive system needs to take into account the decimal role of each digit. In our cats example, the “2” in 26 means two decades, not two units. For any two-digit quantity, the weight of the decade digit should be 10 times the weight of the unit digit. Our study aimed to understand how the brain handle this weighting-according-to-decimal-role challenge.
In our experiment, the participants saw two-digit numbers. To make them translate each digit pair to quantity, we asked them to point to the corresponding position on a 0-100 number line. For example, if you saw 50 you should point to the middle of the line. The idea is that to specify a continuous location on the number line, the participant must first represent the appropriate quantity. This number-line task provides a lot of information. For example, if you placed all numbers within each decade too close to each other (e.g., 50, 51, 52, … 58, 59 are closer than they should be), I may conclude that you ignore the unit digit or at least under-estimate its effect (this is in fact what many children do, even in late elementary school grades). In the present study we used a measurement technique that can tell us how long it took the participant to process each of the number’s digit. I will not get into the details of this technique, which is called finger tracking; if you’re interested, you can read the full article (see link at the bottom of the file) or check out this “granny summary”, which describes the finger-tracking method. For now, you should only know this about the finger tracking method: it measures the gross processing time of each digit. More precisely, the experimenter decides when the digits appear on screen (the digit onset time); the finger-tracking technique allows measuring when a digit has been processed and started affecting the participant’s behaviour (the digit effect time). The digit’s gross processing duration is the digit effect time minus the digit onset time.
In the number-line task, the finger-tracking method showed very consistent results. Across 12 experiments, the processing durations of the decade digit and the unit digit were almost identical to each other: both digits started affecting the participant’s behaviour about 350-400 milliseconds after a 2-digit number was presented on screen. This is a nice finding, but it still doesn’t tell us precisely how two-digit quantities are computed. For example, one interpretation of this finding could be that each digit is processed separately, with identical processing durations for the two digits. Another possibility is that the two digits are processed as a single chunk – i.e., you see “26” and you translate it as a whole into the corresponding quantity. In fact, neither of these two possibilities is correct. Let me tell you how we reached this conclusion.
Our participants saw two-digit numbers, and crucially, the two digits appeared on screen simultaneously only in some cases. In other cases, we manipulated the digit onset times: the decade digit appeared slightly before the unit digit, or vice versa. To understand why this manipulation is useful, consider the two hypotheses from the previous paragraph. First, consider the hypothesis that the digits are processed independently of each other, with identical processing durations. Under this hypothesis, if we delay the onset time of either digit by t milliseconds, the effect time of that digit (measured using our finger-tracking method) should be delayed by the same amount – by t milliseconds. In contrast, if two-digit strings are recognized as wholes, then delaying the onset time of either digit by t milliseconds would delay the effect-time of both digits by t milliseconds.
Figure 1 shows the actual results when we delayed the unit digit onset time (i.e. when the decade digit appeared first, followed by the unit digit). The pattern of results was as follows: first, a very small delay of the unit digit onset (33 milliseconds) did not make any difference: the unit digit effect time was the same as in the case when the decade and unit digits were presented simultaneously. Second, when we delayed the unit onset time by t larger than 33 milliseconds, the unit digit effect time was delayed by slightly less (on average, by t – 35 milliseconds). This pattern agrees with neither of the hypotheses above, so we can say that they were both refuted.
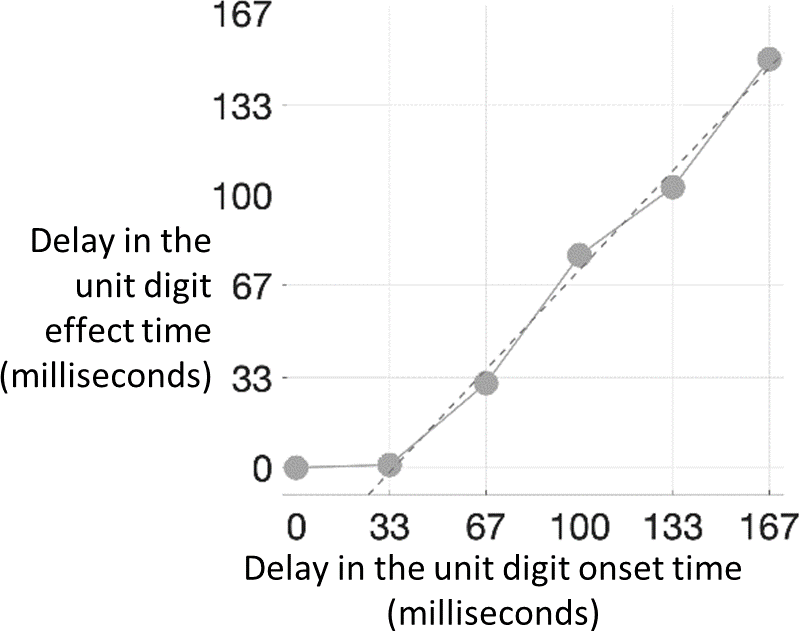
Figure 1. The delay in the unit digit effect time induced by delaying the unit digit onset time.
To understand these results, think about the processing of the decade digit and the unit digits as two separate “processors”. Our results indicate that the “unit processor” does not work all the time; rather, it is idle at some stage for about 35 milliseconds. If we delay the unit digit onset time by less than 35 milliseconds, this would simply shorten the unit processor’s idle time, but the unit digit effect time would remain unchanged. However, if we delay the unit digit onset time by t larger than 35 milliseconds, this would “eat up” the full 35 milliseconds of idle processing, and creates an additional processing delay of t minus 35 the initial idle-time duration, i.e., t – 35 milliseconds.
But why is the “unit processor” idle for 35 milliseconds? What is it waiting for? Our idea is that to translate a multi-digit number to quantity, the brain must prepare itself according to the number of the digits in the number, and create some sort of template that specifies the relative weights of the two per-digit quantities. This template (which we called “syntactic frame”) contains a placeholder for each digit – e.g., for a two-digit number, there would be a decade placeholder, assigned a value of 10, and a unit placeholder, assigned a value of 1. You may think of this template as neural hard-wiring of our knowledge about the decimal system.
How does this template work precisely? What happens with numbers with 3 or more digits? What happens when you present the unit digit first and then the decade? If you want to know, read the full article.
