תקציר-סבתא של המאמר מאת דרור דותן ונדין ברוטמן
Syntactic chunking reveals a core syntactic representation of multi-digit numbers, which is generative and automatic
“You don’t have to be a mathematician to have a feel for numbers.”
— John Nash
השאלה “מהם מספרים” העסיקה את גדולי הפילוסופים במהלך הדורות. למשל, פיתגורס וחסידיו טענו שמספרים הם מה שמסביר את סודות היקום (רעיון שחזר על עצמו גם בסדרת הספרים “מדריך הטרמפיסט לגלקסיה”), והם ממשיים לא פחות מאובייקטים אחרים בעולם. למעלה מ-2,000 שנה אחריו, פילוסוף ידוע אחר – עמנואל קאנט – טען בדיוק ההיפך: המתמטיקה לא קיימת בעולם עצמו, אלא משקפת אוסף תפיסות אנושיות שבאמצעותן אנחנו תופסים את העולם. כיום, אנחנו מסתכלים על השאלה “מהם מספרים” לא רק מנקודת מבט פילוסופית אלא גם מנקודת מבט קוגניטיבית, ושואלים שאלה שכנראה מזכירה יותר את העמדה של קאנט: איך המוח שלנו מבין מספרים? הגישה המקובלת בעשורים האחרונים היא שבני-אדם תופסים מספרים לפחות ב-3 צורות, בעזרת 3 מנגנונים קוגניטיביים נפרדים: מנגנון לתפיסת מילות מספר (“שלוש”); מנגנון לתפיסת ספרוֹת (“3”); ומנגנון לתפיסת כמות לא-סימבולית (“•••”) – מנגנון שנותן לנו את התחושה הבלתי-אמצעית של “כמה הרבה יש פה”. החלוקה הזאת, ל-3 סוגי תפיסת מספרים, נקראת מודל 3 הייצוגים.
יש סיכוי לא רע שאתם חושבים עכשיו לעצמכם שמשהו חסר פה: החלק בו אנחנו באמת מבינים את המספר עצמו. אכן, מודל 3 הייצוגים לא מתאר מנגנון כזה. מבחינתו, אין “הבנת עומק” של המספר. יש 3 ייצוגים למספר וזהו, והצירוף של שלושתם הוא-הוא שנותן לנו את התחושה שאנחנו מבינים את המספר.
יש לא מעט מחקרים שתומכים בטענות של מודל 3 הייצוגים, והסיפור של 3 ייצוגים מחזיק יפה מאד כשאנחנו מדברים על מספרים קטנים – למשל מספרים חד-ספרתיים. אבל כשמגיעים למספרים גדולים יותר העסק מסתבך. במובן מסוים זה אולי לא מפתיע, כי מודל 3 הייצוגים מתעניין בעיקר ברעיון של 3 ייצוגים, ופחות מתעניין במורכבויות הספציפיות של מספרים רב-ספרתיים.
קחו לדוגמה את המספר 42. מודל 3 הייצוגים יגיד, ובצדק, שאפשר לייצג אותו בתור ספרות (42) או מילים (ארבעים ושתיים) או כמות (דמיינו 42 נקודות). אבל יש פה עוד עניין, שהרעיון של 3 ייצוגים אמנם לא סותר אותו אבל גם לא מסביר אותו: אנחנו יודעים ש-42 זה 4 עשרות ו-2 יחידות. בקיצור, אנחנו מבינים את המבנה העשרוני של מספרים.
איפה ואיך בדיוק קורה הדבר הזה, התפיסה של המבנה העשרוני?
המערכת העשרונית היא המצאה גאונית. כיום, מספרים רב-ספרתיים נראים לנו הכי טבעי בעולם, אבל לאנושות לקח המון המון זמן להמציא את הרעיון של place-value – הרעיון שאותה ספרה, אם היא מופיעה במקומות שונים במספר, מייצגת כמויות שונות ובדרך כלל גם אומרים אותה בעזרת מילים שונות. אגב, הראשונים שהמציאו את הרעיון הזה היו כנראה הבבלים, אן כי הם לא השתמשו בבסיס 10 אלא בבסיס 60. וזה לא רק עניין היסטורי: אפילו במאה ה-21, גם אם המערכת העשרונית נראית לכם טבעית, תחשבו שוב. למשל, גם אחרי שילדים למדו את 10 הספרות הראשונות, לוקח להם עוד שנים לא מעטות עד שהם לומדים את העקרון של place-value ואת אופן השימוש במספרים רב-ספרתיים. ואפילו בקרב מבוגרים, יש לא מעט אנשים (להערכתנו לפחות 10% מהאוכלוסיה) שממש מתקשים להתמודד עם מספרים רב-ספרתיים.
כדי לקבל תחושה של הקושי הכרוך בכך, חשבו למשל על המספר 804,720,321,600 – איך אומרים אותו? מה הכמות שהוא מייצג?
התשובה היא שאומרים “שמונה מאות וארבעה מיליארד, שבע מאות ועשרים מיליון, שלוש מאות עשרים ואחד אלף ושש מאות”. חלקכם ידעו לומר את זה (אגב, התלבטתם בין מיליארד לביליון? אתם לא לבד! יש כמה מערכות שונות לשמות של מספרים גדולים), אבל בטוח לקח לכם רגע לחשוב על זה. אני גם מנחש שזה לא קפץ לכם מייד לראש כמו במקרה של 42, אלא השתמשתם באיזושהי אסטרטגיה – למשל לספור כמה ספרות יש במספר. ולגבי הכמות – אתם כנראה מבינים שזה מספר עצום, אולי אפילו אמרתם לעצמכם שזה בערך 1012, אבל עדיין קשה לכם לתפוס אינטואיטיבית את הכמות שהמספר הזה מייצג.
אז מה הסיפור של מספרים רב-ספרתיים? האם אנחנו באמת מבינים אותם ממש באופן אינטואיטיבי כמו שאנחנו מבינים את המספר 3? או שאנחנו לא באמת מבינים אותם אלא רק יודעים אוסף כללים ואסטרטגיות שמאפשרים לנו להשתמש בהם?
נקודת המפתח פה היא מה שאנחנו קוראים לו המבנה התחבירי של המספר – בעצם, אותו היבט של המספר שמשקף את המערכת העשרונית. היכולת לתפוס שבמספר 42 יש ספרת עשרות (שהיא 4) וספרת יחידות (שהיא 2), ובאופן דומה לתפוס שבמספר הארוך שכתבתי יש 12 ספרות, ומה המיקום העשרוני של כל ספרה (ועוד כמה דברים שלא ניכנס אליהם עכשיו). אז היום אני רוצה לספר לכם על מחקר שלנו, שמטרתו היתה לבדוק האם יש לנו תפיסה של מבנה המספר. ולא סתם תפיסה של המאפיינים הבסיסיים (low-level) של מבנה המספר, כמו למשל כמה ספרות יש בו; רצינו לדעת אם יש לנו תפיסה אינטואיטיבית, במילים אחרות ייצוג קוגניטיבי, של המבנה המלא של המספר.
כדי לבדוק זאת, השתמשנו בטריק שמתבסס על מטלת זיכרון פשוטה: השמענו למשתתפים בניסוי רצף של מילות מספר, והם היו צריכים לחזור עליו. הטריק היה שבחלק מהמקרים, רצף המילים היה תחבירי – כלומר המילים התחברו למספר שלם, למשל “מאתיים שבעים וחמש”; ובמקרים אחרים הצגנו בדיוק את אותן מילים, אבל בסדר לא תחבירי, כלומר סדר שלא מתחבר למספר שלם (“חמש שבעים ומאתיים”). הרעיון פשוט מאד: אם המשתתפים זוכרים כל מספר סתם בתור רצף מילים, ואין להם ייצוג של המבנה התחבירי, אז זה לא משנה אם נבקש מהם לזכור רצף תחבירי או לא תחבירי. בשתי הדוגמאות הנ”ל יש 3 מילים בכל רצף, לכן מבחינת אתגר הזיכרון, שתיהן אמורות להיות באותה רמת קושי. לעומת זאת, אם המשתתפים מייצגים את המבנה של המספר, אז מבחינתם יש הבדל משמעותי בין 2 המקרים: במקרה של רצף תחבירי, ורק בו, הם יתפסו את המספר בתור יחידה אחת ולא בתור 3 מילים נפרדות. בעולם של מטלות זיכרון, התהליך הזה נקרא צ’אנקינג (“אורזים” את 3 מילים לצ’אנק אחד), ויש מיליון מחקרים שמראים שצ’אנקינג מאד עוזר לנו לזכור, וספציפית במטלות מהסוג הזה, של חזרה על רשימת מילים. בקיצור, אם המשתתפים מייצגים את המבנה התחבירי של המספר, הם אמורים לזכור טוב יותר את הרצף התחבירי מאשר את הרצף הלא-תחבירי. וזה בדיוק מה שקרה:
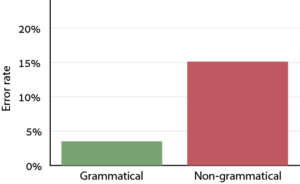
תרשים 1: שיעור הטעויות בחזרה על רצפים תחביריים (ירוק) היה נמוך יותר מאשר בחזרה על רצפים לא-תחביריים (אדום)
אני משער שניחשתם בעצמכם את התשובה עוד לפני שקראתם מהי, כי הרגשתם בעצמכם שזה קל יותר לזכור את הרצף התחבירי מהרצף הלא-תחבירי. הסיבה שהרגשתם בכך היא שהאפקט הזה הוא לא זניח – הוא באמת מאד חזק, וזה קצת משכנע אותנו שהייצוג הזה, של מבנה המספר, הוא באמת חזק ומשמעותי.
המחקר לימד אותנו שכשאנחנו תופסים מספרים, אנחנו תופסים לא רק את הספרות והמילים, אלא גם את המבנה התחבירי/העשרוני של המספר. יותר מכך: לא רק שאנחנו יודעים בתאוריה את המבנה העשרוני, ויודעים לחלץ מהמספר מידע שרלוונטי למבנה הזה (למשל כמה ספרות היו בו), אלא יש לנו ממש איזשהו ייצוג קוגניטיבי של המבנה המלא של המספר.
איך בדיוק נראה הייצוג הזה במוח, איך אנחנו בונים אותו, ומה המשמעות של זה לגבי השיטה הרצויה ללמידת המערכת העשרונית בביה”ס? המחקר שלנו נתן תשובה חלקית לכך, אבל גם השאיר הרבה שאלות פתוחות. מתעניינים? מוזמנים לקרוא את הפרטים במאמר.
